硬件姿态解算

四轴的姿态解算无疑是最繁琐的步骤没有之一，但是自从MPU6050出现了硬件DMP的时候，大妈都能完成姿态解算了！

CrazePony使用了MPU6050自带的硬件四元数单元，可以通过IIC直接读取四元数，省却了软件解算繁琐的算法步骤，非常方便易用。

这里还是要首先介绍下四元数，四元数要说的实在太多，因为它的优点很多，利用起来很方便，但是理解起来就有点蹩脚了。我们百度四元数，一开始看到的就是四元数来历，还有就是四元数的基本计算。对于来历，还是想说一下，四元数（Quaternions）是由威廉·卢云·哈密尔顿(William RowanHamilton,1805-1865）在1843 年爱尔兰发现的数学概念。

将实数域扩充到复数域，并用复数来表示平面向量，用复数的加、乘运算表示平面向量的合成、伸缩和旋，这就是我们熟知的复数的二维空间含义，所以人们会继续猜想，利用三维复数不就可以表达三维空间的变换了吗，历史上有很多数学家试图寻找过三维的复数，但后来证明这样的三维复数是不存在的。有关这个结论的证明，我没有查到更明确的版本，据《古今数学思想》中的一个理由，三维空间中的伸缩旋转变换需要四个变量来决定：两个变量决定轴的方向，一个变量决定旋转角度，一个变量决定伸缩比例。这样，只有三个变量的三维复数无法满足这样的要求。但是历史上得到的应该是比这个更强的结论，即使不考虑空间旋转，只从代数角度来说，三维的复数域作为普通复数域的扩张域是不存在的。并且，据《古今数学思想》叙述，即使像哈密尔顿后来引入四元数那样，牺牲乘法交换律，这样的三维复数也得不到。经过一些年的努力之后， Hamilton 发现自己被迫应作两个让步，第一个是他的新数包含四个分量，而第二个是他必须牺牲乘法交换律。（ 《古今数学思想》第三册177 页）但是四元数用作旋转的作用明显，简化了运算，而且避免了Gimbal Lock，四元数是最简单的超复数，我们不能把四元数简单的理解为3D 空间的矢量，它是4 维空间中的的矢量，也是非常不容易想像的。

我们知道在平面(x,y)中的旋转可以用复数来表示，同样的三维中的旋转可以用单位四元数来描述。我们来定义一个四元数：

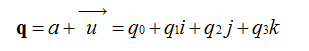
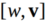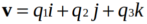我们可以把它写成，其中，。那么V是矢量，表示三维空间中的旋转轴。w是标量，表示旋转角度。那么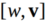就是绕轴V旋转w度，所以一个四元数可以表示一个完整的旋转。只有单位四元数才可以表示旋转，至于为什么，因为这就是四元数表示旋转的约束条件。

所以大家可以理解为，单位四元数能够表示旋转。我们给出一组单位四元数和欧拉角的转换关系，通过这个关系来将采集到的四元数转化成欧拉角，原理将在软件解算中给出，这里直接使用就可以了：

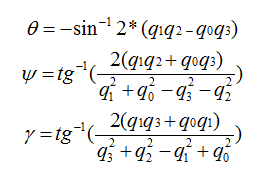
所以在四轴飞行器中，传感器读取到四元数，首先应先将它归一化成单位四元数：

norm = dmpinvSqrt(q[0]*q[0] + q[1]*q[1] + q[2]*q[2] + q[3]*q[3]);
q[0] = q[0] * norm;
q[1] = q[1] * norm;
q[2] = q[2] * norm;
q[3] = q[3] * norm;

归一化后根据四元数和欧拉角转换公式把四元数转化为欧拉角，OK,硬件姿态解算完成！

DMP_DATA.dmp_roll = (atan2(2.0*(q[0]*q[1] + q[2]*q[3]), 1 - 2.0*(q[1]*q[1] + q[2]*q[2])))* 180/M_PI;
// we let safe_asin() handle the singularities near 90/-90 in pitch
DMP_DATA.dmp_pitch = dmpsafe_asin(2.0*(q[0]*q[2] - q[3]*q[1]))* 180/M_PI;

DMP_DATA.dmp_yaw = -atan2(2.0*(q[0]*q[3] + q[1]*q[2]), 1 - 2.0*(q[2]*q[2] + q[3]*q[3]))* 180/M_PI;